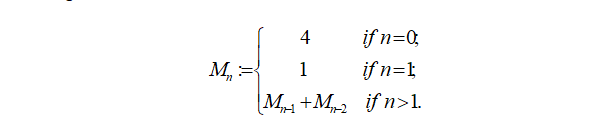Our brief Journey with some properties and patterns of the Mulatu Numbers
Abstract
The Mulatu numbers were introduced by Mulatu Lemma in [1]. The Mulatu numbers are integral sequences of numbers of the form: 4, 1, and 5,6,11,17,28,45...These numbers have wonderful and amazing properties and patterns.
In mathematical terms, the sequence of the Mulatu numbers is defined by the following recurrence relation:
The first number of the sequence is 4, the second number is 1, and each subsequent number is equal to the sum of the previous two numbers of the sequence itself. That is, after two starting values, each number is the sum of the two preceding numbers. In [1] some properties and patterns of the numbers were considered. In this paper, we more deeply examine additional properties and patterns of these fascinating and mysterious numbers. Many beautiful mathematical identities involving the Mulatu numbers, the Fibonacci numbers, and the Lucas numbers will be explored.
2000 Mathematical Subject Classification: 11
Downloads
References
Burton, D. M.,Elementary number theory. New York City, New York: McGraw-Hill. 1998.
Copyright (c) 2021 GPH - International Journal of Mathematics

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
The authors and co-authors warrant that the article is their original work, does not infringe any copyright, and has not been published elsewhere. By submitting the article to GPH - International Journal of Mathematics, the authors agree that the journal has the right to retract or remove the article in case of proven ethical misconduct.