ON THE NORM OF JORDAN ELEMENTARY OPERATOR IN TENSOR PRODUCT OF C*-ALGEBRAS

  • Peter Guchu Muiruri Department of Physical Sciences,Chuka University, Chuka, Kenya
  • Denis Njue King'ang'i Department of Mathematics and Computer Science, University of Eldoret, Eldoret, Kenya
  • Sammy Wabomba Musundi Department of Physical Sciences,Chuka University, Chuka, Kenya
DOI: https://doi.org/10.5281/zenodo.10794296
Keywords: Jordan Elementary Operator, Finite Rank Operator, Tensor Product, Operators and C*-algebras

Abstract

The norm property of different types of Elementary operators has attracted a lot of researchers due to its wide range applications in functional analysis. From available literature the norm of Jordan elementary operator has been determined in C*-algebras, JB*-algebras,standard operator algebra and prime JB*-triple but not much has been done in tensor product of C*-algebras. This paper, dealt with the norm of Jordan elementary operator in a tensor product of C*-algebras. More precisely, the paper investigated the bounds of the norm of Jordan elementary operator in a tensor product of C*-algebras and obtained that 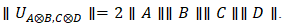formula.PNGThe concept of finite rank operator and properties of tensor product of Hilbert spaces and operators and vectors in Hilbert spaces were used to achieve the paper’s objective.

Downloads

Download data is not yet available.

References

[1] Barraa, M. and Boumazgour, M. (2001). A Lower Bound of the Norm of the Operator . ExtractaMathematicae, 16(2):223–227.
[2] Blanco, A., Boumazgour, M., and Ransford, T. (2004). On the Norm of Elementary Operators. Journal of the London Mathematical Society, 70(2):479–498.
[3] Bunce, L., Chu, C., Stachó, L., and Zalar, B. (1998). On Prime JB*-triples. Quarterly Journal of Mathematics, 49(195):279–290.
[4] Daniel, B., Musundi, S., and Ndungu, K. (2022). Application of Maximal Numerical Range on Norm of Basic Elementary Operator in a Tensor Product. Journal of Progressive Research in Mathematics, 19(1) :73-81.
[5] Daniel, B., Musundi, S., and Ndungu, K. (2023). Application of Maximal Numerical Range on Norm of Elementary Operator of length Two in a Tensor Product. International Journal of Mathematics and Computer Research, 11 :3837-3842.
[6] Garcia, M. C. and Palacios, A. R. (1994). Non-degenerately Ultraprime Jordan–Banach Al-gebras: A Zel’Manovian Treatment. Proceedings of the London Mathematical Society,3(3):576–604.
[7] Mathieu, M. (1990). More Properties of the Product of Two Derivations of a C*-algebra.Bulletin of the Australian Mathematical Society, 42(1):115–120.
[8] Muiruri, P., Denis, N., and Sammy, W. (2018). On Norm of Basic Elementary Operator in a Tensor Product. International Journal of Science and Innovation Mathematics Research, 6(6) :15-22.
[9] Muiruri, P., Denis, N., and Sammy, W. (2024). On Norm of finite length Elementary Operator in a Tensor Product of C*-algebras. International Journal of Mathematics and Computer Research, 12:3991-3995.
[10] Stacho, L. and Zalar, B. (1998). Uniform Primeness of the Jordan Algebra of Symmetric Operators. Proceedings of the American Mathematical Society, 126(8):2241–2247.
[11] Stachó, L. L. and Zalar, B. (1996). On the norm of Jordan Elementary Operators in Standard Operator Algebras. PublicationesMathematicae Debrecen, 49(1-2):127–134.
Published
2024-03-06
How to Cite
Muiruri, P. G., King’ang’i, D. N., & Musundi, S. W. (2024). ON THE NORM OF JORDAN ELEMENTARY OPERATOR IN TENSOR PRODUCT OF C*-ALGEBRAS. GPH-International Journal of Mathematics, 7(03), 01-10. https://doi.org/10.5281/zenodo.10794296
Issue
Vol 7 No 03 (2024): GPH - International Journal of Mathematics
Section
Articles
Copyright (c) 2024 Muiruri P.M, King’ang’I D.N, Musundi S.W

The authors and co-authors warrant that the article is their original work, does not infringe any copyright, and has not been published elsewhere. By submitting the article to GPH - International Journal of Mathematics, the authors agree that the journal has the right to retract or remove the article in case of proven ethical misconduct.