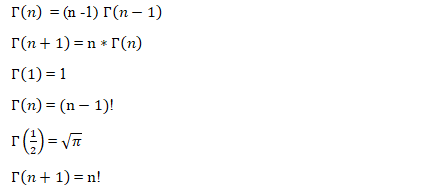The Fascinating Gamma Function in actions
Abstract
The gamma function has several properties that define it. In this paper, I will present proofs for those properties and give example using real numbers. The properties I will prove are as followed:
Downloads
References
G.E. Andrews, R. Askey and R. Roy, Special functions, Cambridge University Press, Cambridge, (1999)
E. Artin, The Gamma Function, New York, Holt, Rinehart and Winston, (1964)
E.W. Barnes, The theory of the gamma function, Messenger Math. (2), (1900), vol. 29, p. 64-128.
P.M Binet, Journal ´ecole polyt., (1839), vol. 16, p. 131
H. Bohr and I. Mollerup, Loerbog I matematisk Analyse, Kopenhagen,
Copyright (c) 2021 GPH - International Journal of Mathematics

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Author(s) and co-author(s) jointly and severally represent and warrant that the Article is original with the author(s) and does not infringe any copyright or violate any other right of any third parties, and that the Article has not been published elsewhere. Author(s) agree to the terms that the GPH Journal will have the full right to remove the published article on any misconduct found in the published article.